Plot a one-dimensional, user-defined function

plot_function(
  f,
  lower,
  upper,
  derivative = FALSE,
  optimize = FALSE,
  maximum = FALSE,
  roots = FALSE,
  optim = FALSE,
  ...
)

Arguments

f	a single-line function
lower	an integer indicating the lower bound
upper	an integer indicating the upper bound
optimize	optimize the function and plot the optimum and FOC (defaults to FALSE). If TRUE it defaults to finding the global minimum. Set `maximum = TRUE` to find the global maximum.
roots	find and plot the roots over the given domain (defaults to FALSE)
optim	use `optim()` to find optima (defaults to FALSE and uses `optimize()` which only implements Brent optimization)
...	additional arguments passed to `optim()` if `optim = TRUE`
maximize	if `optimize = TRUE` find the maximum (defaults to FALSE and finds the minimum)

Value

ggplot object

Author

Lawrence R. De Geest

Examples

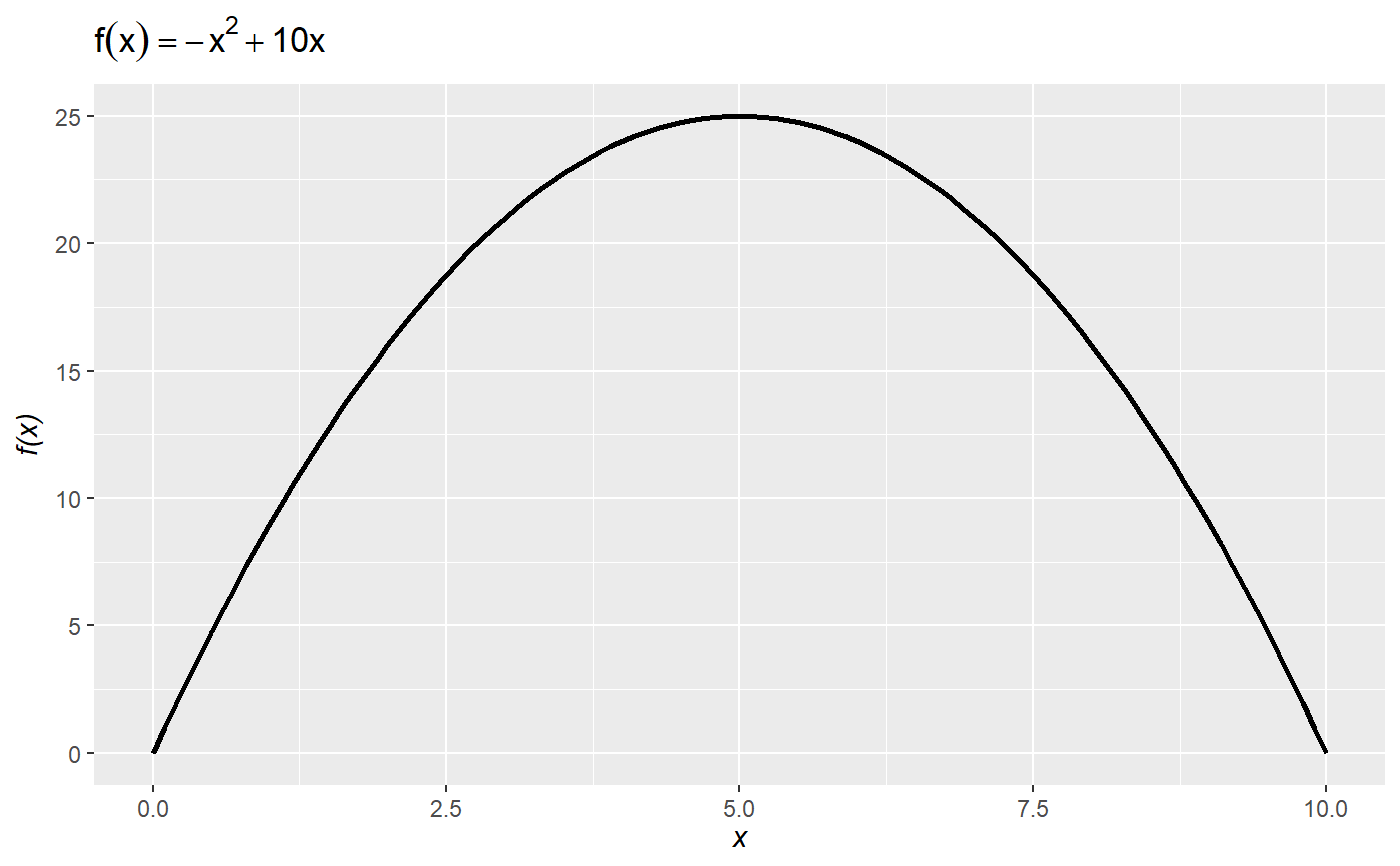
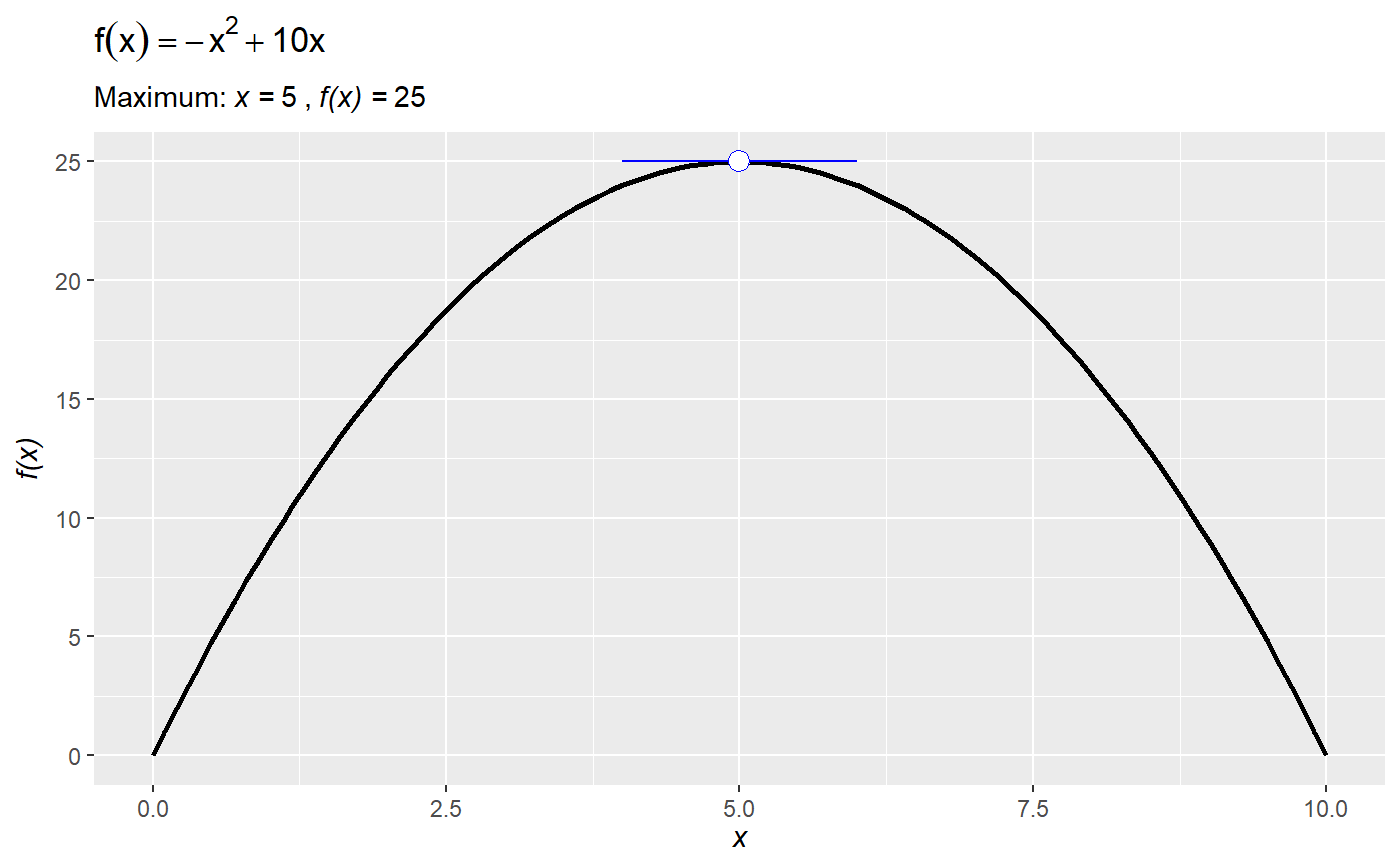
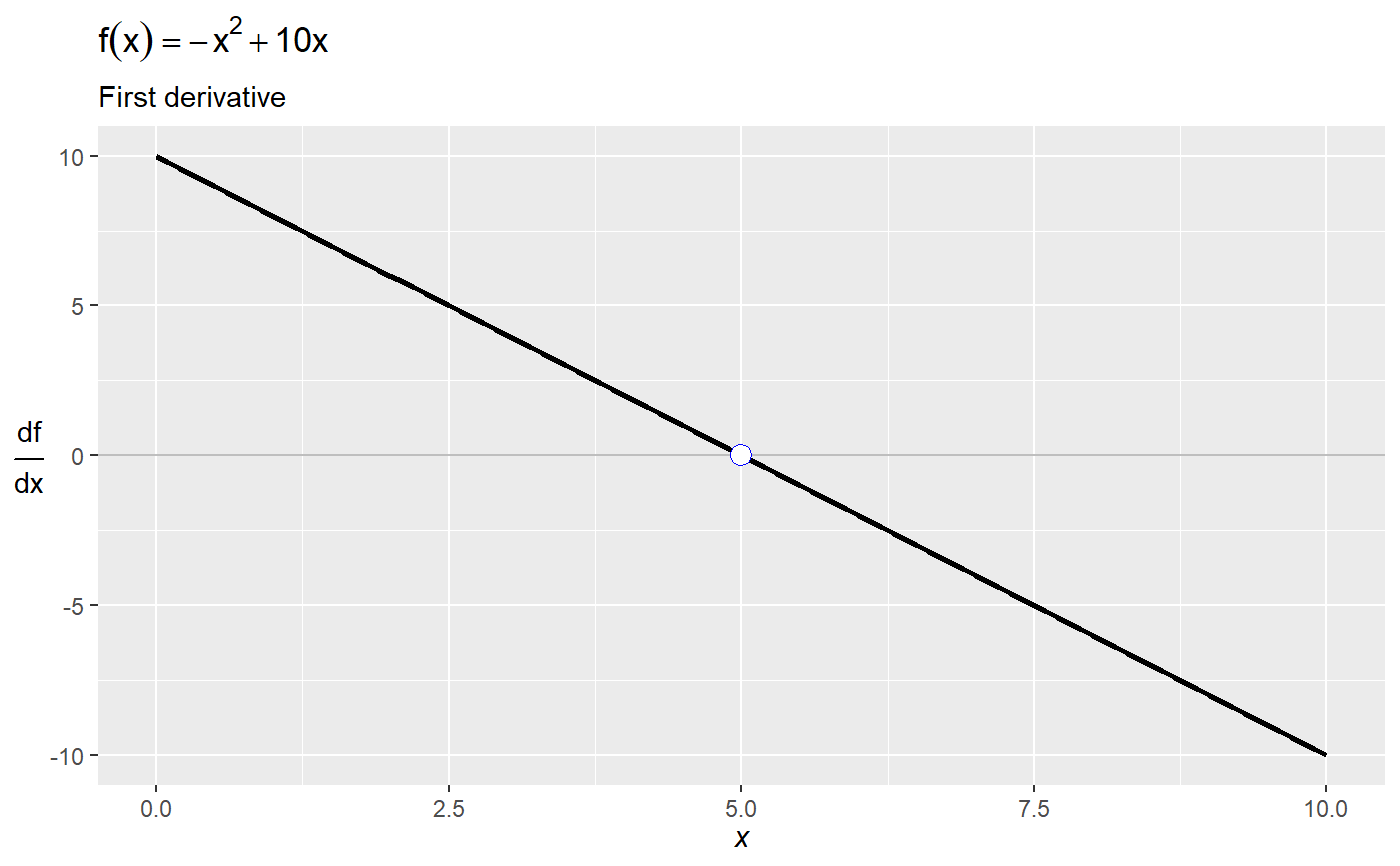
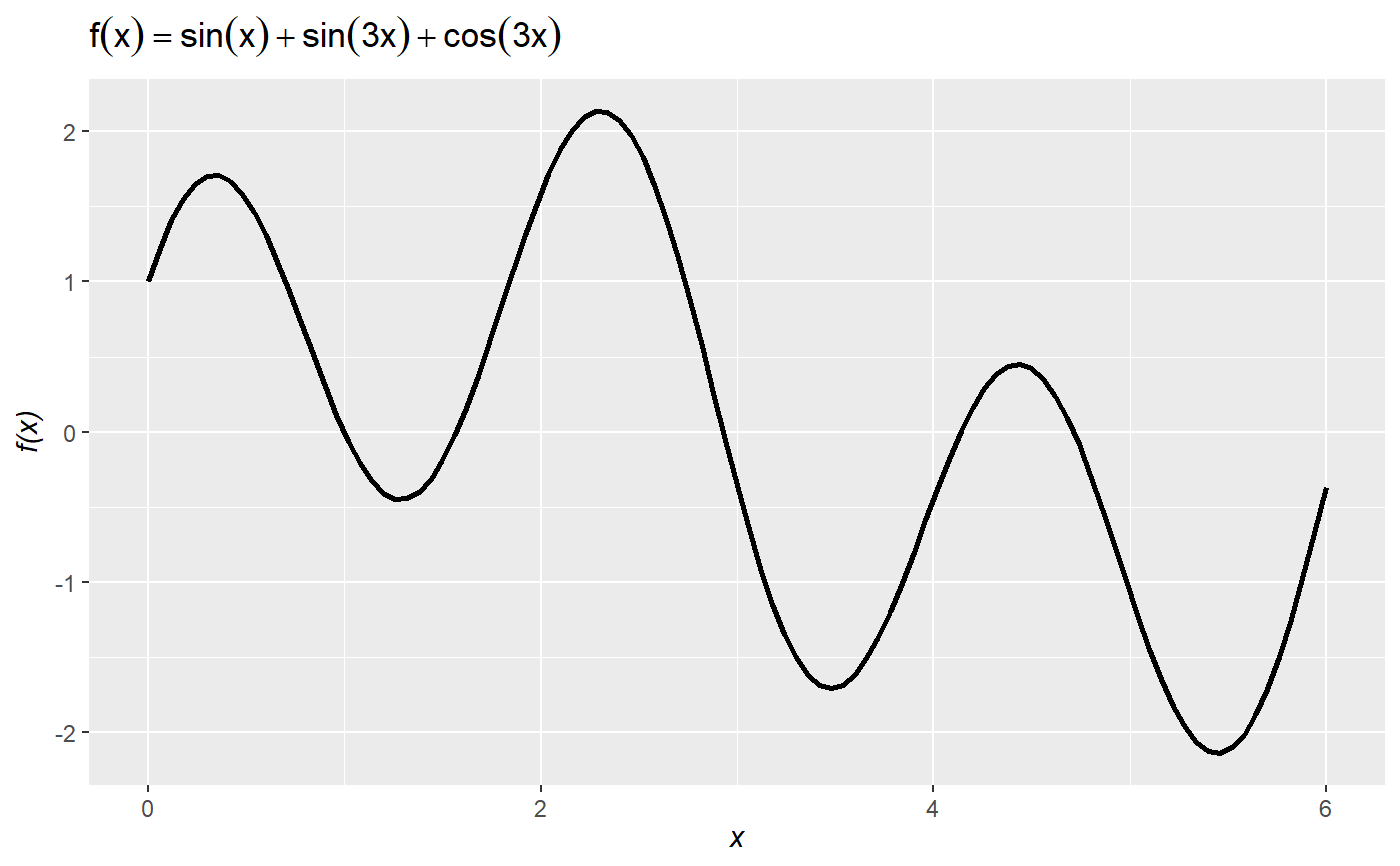
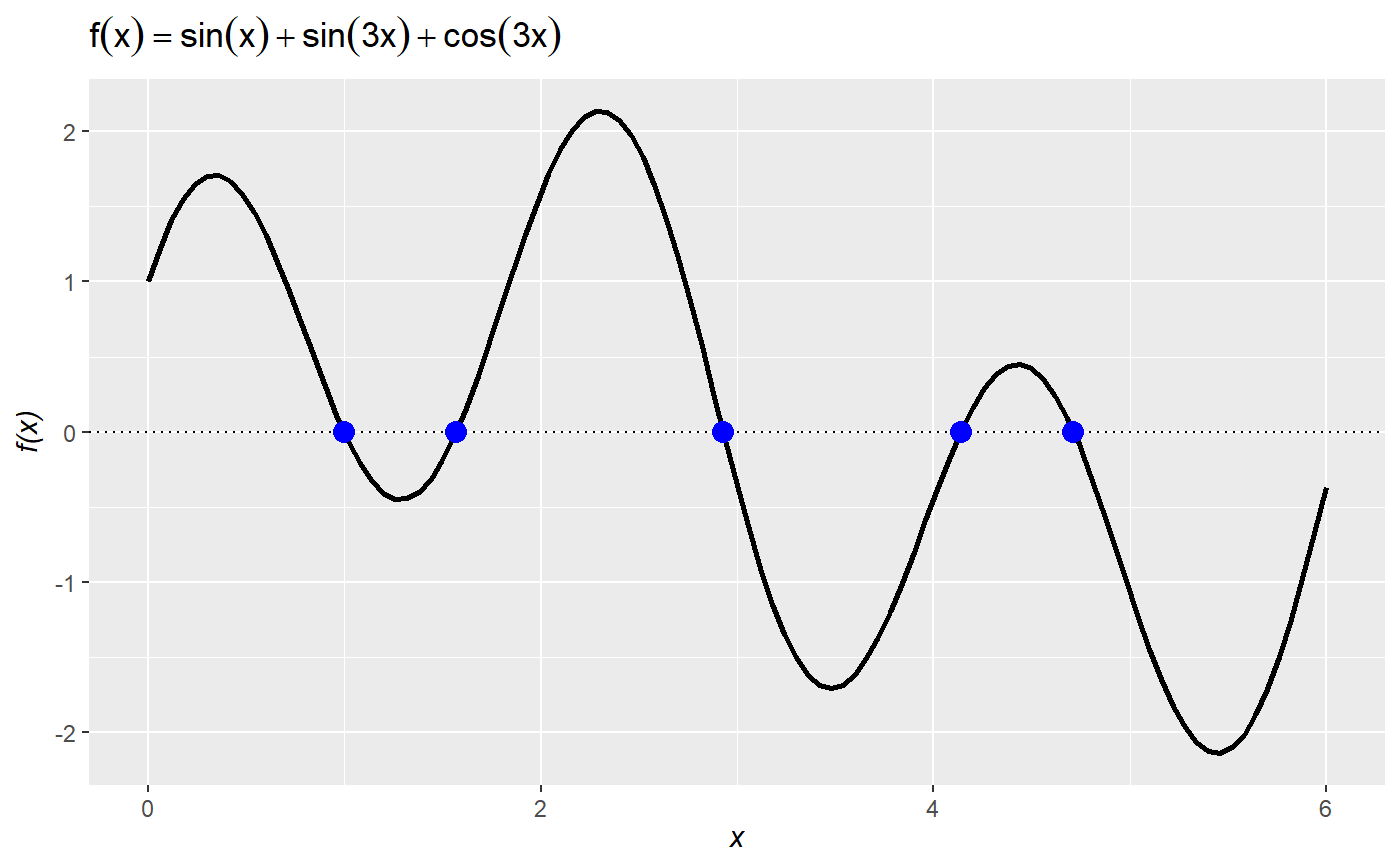
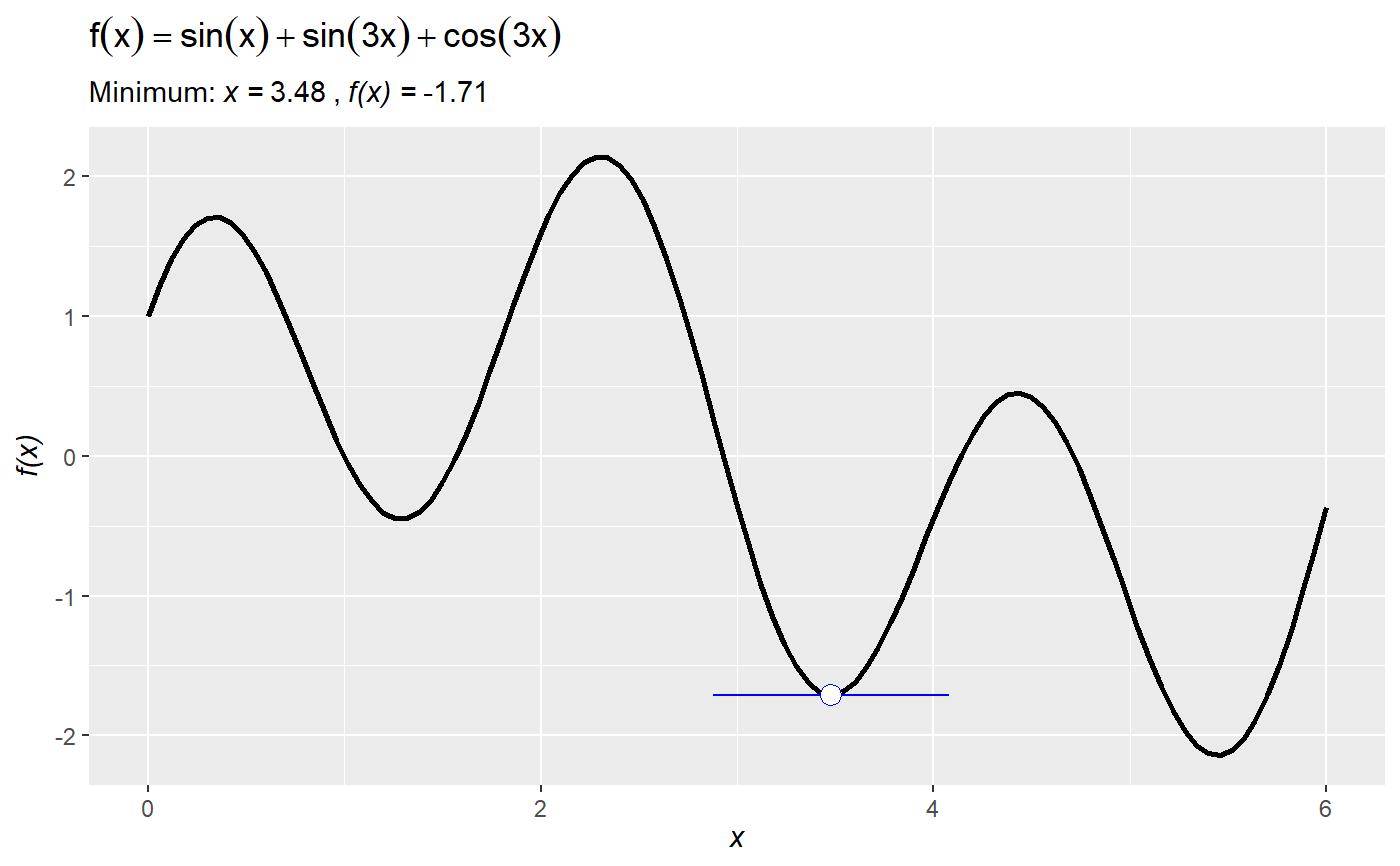
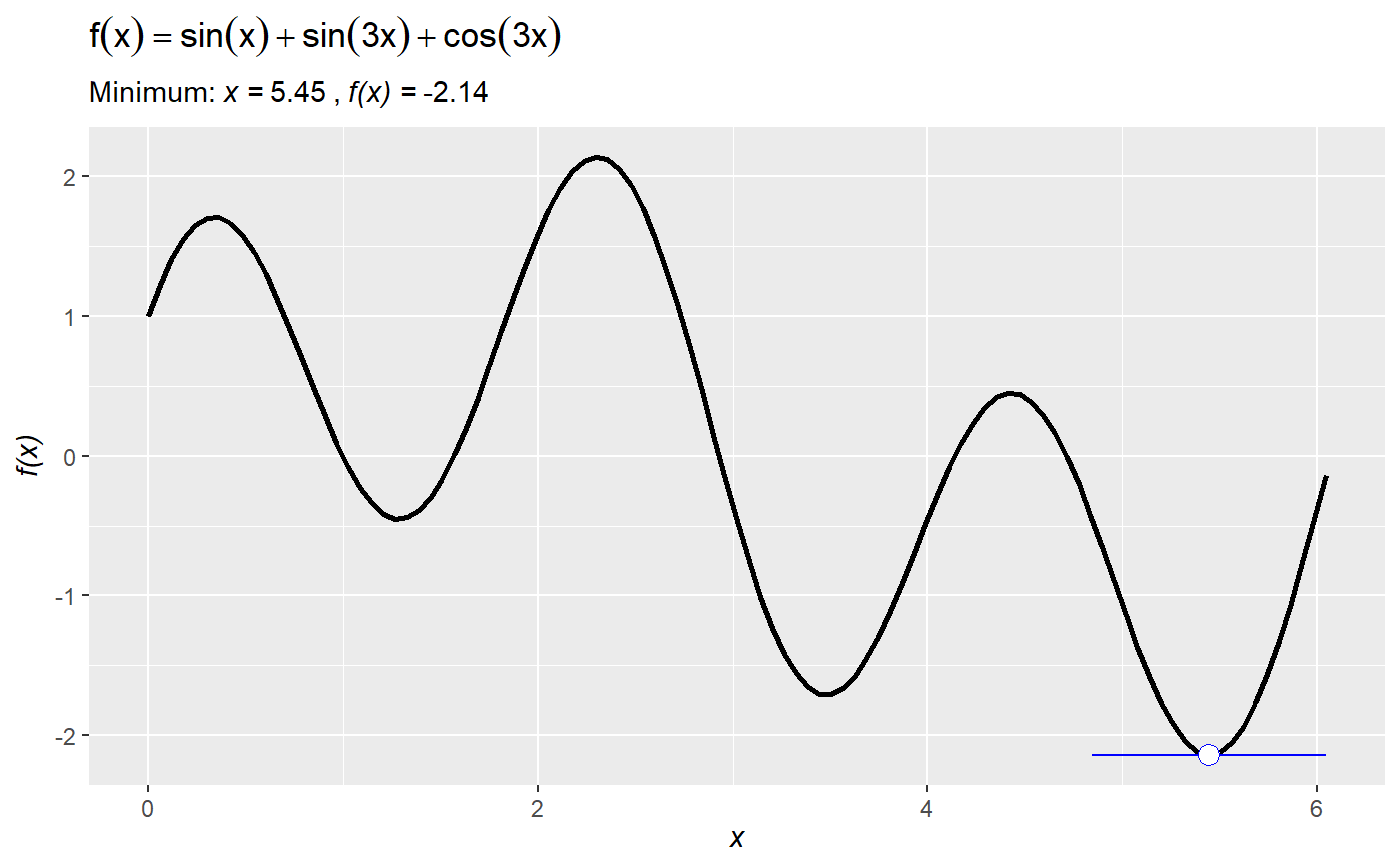
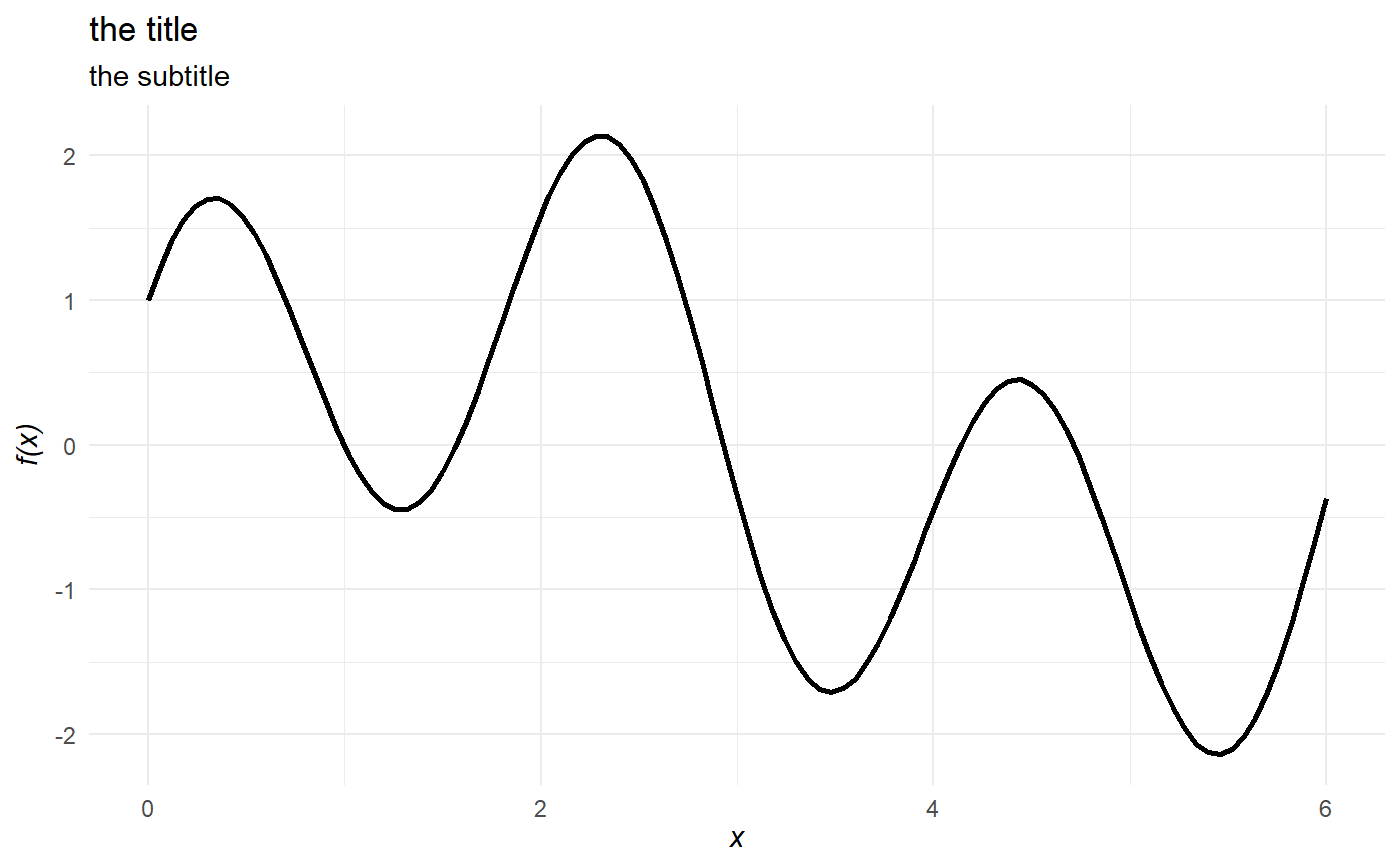
# declare some function
## right now the function needs to be declared on a single line
f = function(x) -x^2 + 10*x
# plot the function over the domain x = {0, ..., 10}
plot_function(f, lower = 0, upper = 10)

# calculate and show the global maximum over the domain. Default is minimization, so set maximum to TRUE:
plot_function(f, lower = 0, upper = 10, optimize = TRUE, maximum = TRUE)

# show that the optimal point occurs where the derivative is zero (i.e., the first-order condition):
plot_function(f, lower = 0, upper = 10, derivative = TRUE, roots = TRUE)

# you can also define an anonymous function (i.e., define a function on the fly *inside* `plot_function`):
plot_function(function(x) sin(x) + sin(3*x) + cos(3*x), lower = 0, upper = 6)

# and show all roots over the domain:
plot_function(function(x) sin(x) + sin(3*x) + cos(3*x), lower = 0, upper = 6, roots = TRUE)

# plot_function uses uses `optimize()` by default, which implements Brent optimization. 
# It can struggle to find local optima for messy functions.
# For instance, it misses the local optimum:
plot_function(function(x) sin(x) + sin(3*x) + cos(3*x), lower = 0, upper = 6, optimize = TRUE)

# you can switch to `optim()` and then set the starting value `par` (from `optim`) to get better results:
plot_function(function(x) sin(x) + sin(3*x) + cos(3*x), lower = 0, upper = 6, optimize = TRUE, optim = TRUE, par = 5)

# since `plot_function` returns a ggplot object you can add ggplot stuff (e.g., change the theme, the titles, etc.)
plot_function(function(x) sin(x) + sin(3*x) + cos(3*x), lower = 0, upper = 6) +
    theme_minimal() +
    labs(subtitle = "the subtitle", title = "the title")